Just as the sine and cosine functions give a parametric equation for the ellipse, so the hyperbolic sine and hyperbolic cosine give a parametric equation for the hyperbola.
As
one has for any value of
 that the point
that the pointWhen μ varies over the interval
 one gets with this formula all points
one gets with this formula all points  on the right branch of the hyperbola.
on the right branch of the hyperbola.The left branch for which
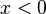 is in the same way obtained as
is in the same way obtained as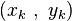 given by
given by




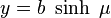
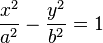



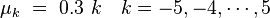
0 comments:
Post a Comment