A hyperbola can also be defined as a second-degree equation in the Cartesian coordinates (x, y) of the plane
provided that the constants Axx, Axy, Ayy, Bx, By, and C satisfy the determinant condition
A special case of a hyperbola—the degenerate hyperbola consisting of two intersecting lines—occurs when another determinant is zero
This determinant Δ is sometimes called the discriminant of the conic section.
Given the above general parametrization of the hyperbola in Cartesian coordinates, the eccentricity can be found using the formula in Conic section#Eccentricity in terms of parameters of the quadratic form.
The center (xc, yc) of the hyperbola may be determined from the formulae
In terms of new coordinates, ξ = x − xc and η = y − yc, the defining equation of the hyperbola can be written
The principal axes of the hyperbola make an angle Φ with the positive x-axis that equals
Rotating the coordinate axes so that the x-axis is aligned with the transverse axis brings the equation into its canonical form
The major and minor semiaxes a and b are defined by the equations
where λ1 and λ2 are the roots of the quadratic equation
For comparison, the corresponding equation for a degenerate hyperbola is
The tangent line to a given point (x0, y0) on the hyperbola is defined by the equation
where E, F and G are defined
The normal line to the hyperbola at the same point is given by the equation
The normal line is perpendicular to the tangent line, and both pass through the same point (x0, y0).
From the equation
the basic property that with 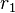 and
and 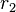 being the distances from a point
being the distances from a point 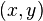 to the left focus
to the left focus 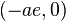 and the right focus
and the right focus 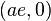 one has for a point on the right branch that
one has for a point on the right branch that
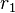 and
and 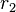 being the distances from a point
being the distances from a point 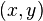 to the left focus
to the left focus 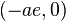 and the right focus
and the right focus 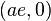 one has for a point on the right branch that
one has for a point on the right branch that
and for a point on the left branch that
can be proved as follows:
If x,y is a point on the hyperbola the distance to the left focal point is
To the right focal point the distance is
If x,y is a point on the right branch of the hyperbola then 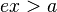 and
and
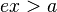 and
and
Subtracting these equations one gets
If x,y is a point on the left branch of the hyperbola then 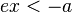 and
and
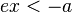 and
and
Subtracting these equations one gets




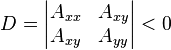


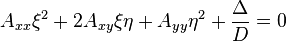


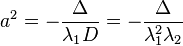
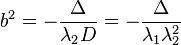
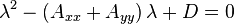
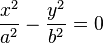
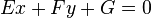
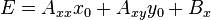
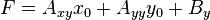
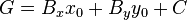
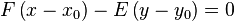
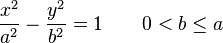
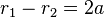
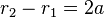
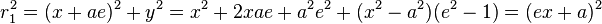
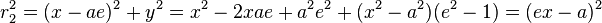

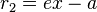
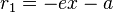
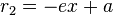
0 comments:
Post a Comment