The x-coordinate at the vertex is 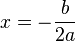 , which is found by differentiating the original equation
, which is found by differentiating the original equation 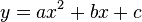 , setting the resulting
, setting the resulting 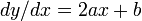 equal to zero (a critical point), and solving for
equal to zero (a critical point), and solving for  . Substitute this x-coordinate into the original equation to yield:
. Substitute this x-coordinate into the original equation to yield:
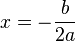 , which is found by differentiating the original equation
, which is found by differentiating the original equation 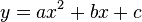 , setting the resulting
, setting the resulting 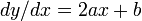 equal to zero (a critical point), and solving for
equal to zero (a critical point), and solving for  . Substitute this x-coordinate into the original equation to yield:
. Substitute this x-coordinate into the original equation to yield:


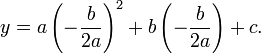

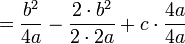
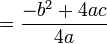
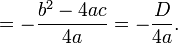
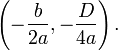
0 comments:
Post a Comment