Applications of Hyperbola

 

1.Sundials

Hyperbolas may be seen in many sundials. On any given day, the sun revolves in a circle on the celestial sphere, and its rays striking the point on a sundial traces out a cone of light. The intersection of this cone with the horizontal plane of the ground forms a conic section. At most populated latitudes and at most times of the year, this conic section is a hyperbola. In practical terms, the shadow of the tip of a pole traces out a hyperbola on the ground over the course of a day (this path is called the declination line). The shape of this hyperbola varies with the geographical latitude and with the time of the year, since those factors affect the cone of the sun's rays relative to the horizon. The collection of such hyperbolas for a whole year at a given location was called a pelekinon by the Greeks, since it resembles a double-bladed axe.

 

Hyperbolas as declination lines on a sundial

2.Trilateration

A hyperbola is the basis for solving trilateration problems, the task of locating a point from the differences in its distances to given points — or, equivalently, the difference in arrival times of synchronized signals between the point and the given points. Such problems are important in navigation, particularly on water; a ship can locate its position from the difference in arrival times of signals from a LORAN or GPS transmitters. Conversely, a homing beacon or any transmitter can be located by comparing the arrival times of its signals at two separate receiving stations; such techniques may be used to track objects and people. In particular, the set of possible positions of a point that has a distance difference of 2a from two given points is a hyperbola of vertex separation 2a whose foci are the two given points.

3.Path followed by a particle

The paths followed by any particle in the classical Kepler problem is a conic section. In particular, if the total energy E of the particle is greater than zero (i.e., if the particle is unbound), the path of such a particle is a hyperbola. This property is useful in studying atomic and sub-atomic forces by scattering high-energy particles; for example, the Rutherford experiment demonstrated the existence of an atomic nucleus by examining the scattering of alpha particles from gold atoms. If the short-range nuclear interactions are ignored, the atomic nucleus and the alpha particle interact only by a repulsive Coulomb force, which satisfies the inverse square law requirement for a Kepler problem.

4.Korteweg-de Vries equation

The hyperbolic trig function  appears as one solution to the Korteweg-de Vries equation which describes the motion of a soliton wave in a canal.

5.Angle trisection

As shown first by Apollonius of Perga, a hyperbola can be used to trisect any angle, an intensely studied problem of geometry. Given an angle, one first draws a circle centered on its middle point O, which intersects the legs of the angle at points A and B. One next draws the line through A and B and constructs a hyperbola of eccentricity ε=2 with that line as its transverse axis and B as one focus. The directrix of the hyperbola is the bisector of AB, and for any point P on the hyperbola, the angle ABP is twice as large as the angle BAP. Let P be a point on the circle. By the inscribed angle theorem, the corresponding center angles are likewise related by a factor of two, AOP = 2×POB. But AOP+POB equals the original angle AOB. Therefore, the angle has been trisected, since 3×POB = AOB.

6.Efficient portfolio frontier

In portfolio theory, the locus of mean-variance efficient portfolios (called the efficient frontier) is the upper half of the east-opening branch of a hyperbola drawn with the portfolio return's standard deviation plotted horizontally and its expected value plotted vertically; according to this theory, all rational investors would choose a portfolio characterized by some point on this locus.

7.Stones in a Lake

When two stones are thrown simultaneously into a pool of still water, ripples move outward in concentric circles. These circles intersect in points which form a curve known as the hyperbola.

8.Cooling Towers of Nuclear Reactors

The hyperboloid is the design standard for all nuclear
cooling towers. It is structurally sound and can be built with straight steel beams.

When designing these cooling towers, engineers are faced with two problems:
(1) the structutre must be able to withstand high winds and
(2) they should be built with as little material as possible.

The hyperbolic form solves both of these problems. For a given diameter and height of a tower and a given strength, this shape requires less material than any other form. A 500 foot tower can be made of a reinforced concrete shell only six or eight inches wide. See the pictures below (this nuclear power plant is located in Indiana).



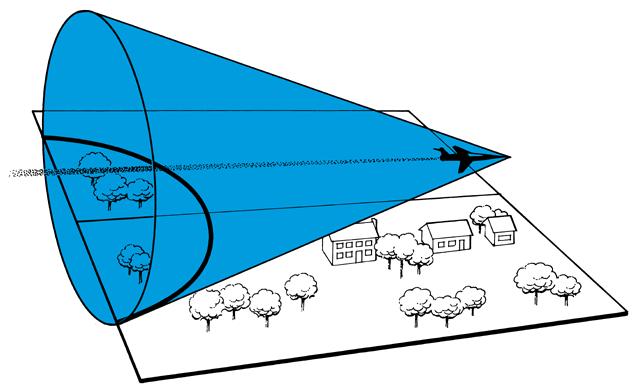
9.Sonic Boom

In 1953, a pilot flew over an Air Force Base flying faster than the speed of sound. He damaged every building on the base.

As the plane moves faster than the speed of sound, you get a cone-like wave. Where the cone intersects the ground, it is an hyperbola.

The sonic boom hits every point on that curve at the same time. No sound is heard outside the curve. The

hyperbola is known as the "Sonic Boom Curve." In the picture below, the sonic boom is "visible" due to the humidity.

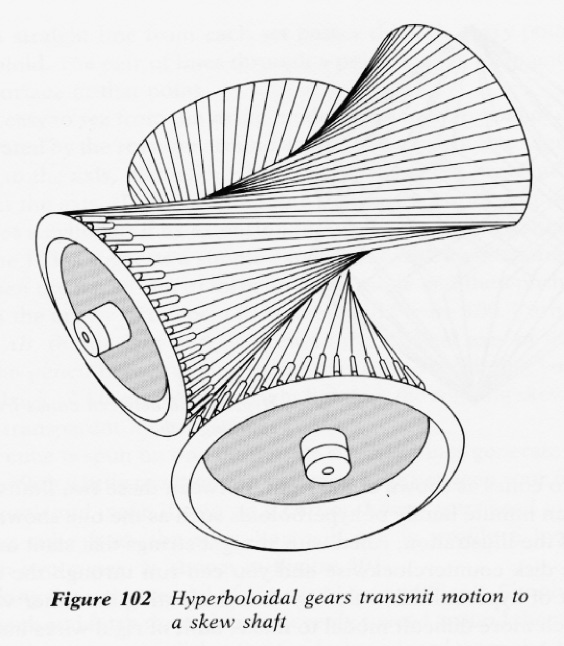
10.Gear transmission

Two hyperboloids of revolution can provide gear transmission between two skew axes. The cogs of each gear are a set of generating straight lines.

 

11.Lampshade

A household lamp casts hyperbolic shadows on a wall. just like..

 

12.Dulles Airport

Dulles Airport, designed by Eero Saarinen, is in the shape of a hyperbolic paraboloid. The hyperbolic paraboloid is a three-dimensional  curve that is a hyperbola in one cross-section, and a parabola in another cross section.