skip to main |
skip to sidebar
Properties of hyperbolas
- If a line intersects one branch of a hyperbola at M and N and intersects the asymptotes at P and Q, then MN has the same midpoint as PQ.
- The following are concurrent: (1) a circle passing through the hyperbola's foci and centered at the hyperbola's center; (2) either of the lines that are tangent to the hyperbola at the vertices; and (3) either of the asymptotes of the hyperbola.
- The following are also concurrent: (1) the circle that is centered at the hyperbola's center and that passes through the hyperbola's vertices; (2) either directrix; and (3) either of the asymptotes.
- The product of the distances from a point P to one of the asymptotes along a line parallel to the other asymptote, and to the second asymptote along a line parallel to the first asymptote, is independent of the location of point P on the hyperbola. If the hyperbola is written in canonical form
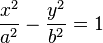 then this product is
then this product is  .
.
- The product of the perpendicular distances from a point P on the hyperbola
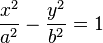 or on its conjugate hyperbola
or on its conjugate hyperbola  to the asymptotes is a constant independent of the location of P: specifically,
to the asymptotes is a constant independent of the location of P: specifically,  , which also equals
, which also equals  where e is the eccentricity of the hyperbola
where e is the eccentricity of the hyperbola 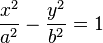 .
.
- The product of the slopes of lines from a point on the hyperbola to the two vertices is independent of the location of the point.
- A line segment between the two asymptotes and tangent to the hyperbola is bisected by the tangency point.
- The area of a triangle two of whose sides lie on the asymptotes, and whose third side is tangent to the hyperbola, is independent of the location of the tangency point. Specifically, the area is ab, where a is the semi-major axis and b is the semi-minor axis.
- The distance from either focus to either asymptote is b, the semi-minor axis; the nearest point to a focus on an asymptote lies at a distance from the center equal to a, the semi-major axis. Then using the Pythagorean theorem on the right triangle with these two segments as legs shows that
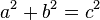 , where c is the semi-focal length (the distance from a focus to the hyperbola's center).
, where c is the semi-focal length (the distance from a focus to the hyperbola's center).
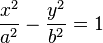 then this product is
then this product is  .
. 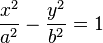 or on its conjugate hyperbola
or on its conjugate hyperbola  to the asymptotes is a constant independent of the location of P: specifically,
to the asymptotes is a constant independent of the location of P: specifically,  , which also equals
, which also equals  where e is the eccentricity of the hyperbola
where e is the eccentricity of the hyperbola 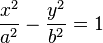 .
.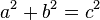 , where c is the semi-focal length (the distance from a focus to the hyperbola's center).
, where c is the semi-focal length (the distance from a focus to the hyperbola's center).


0 comments:
Post a Comment