Cartesian
In the following equations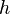 and
and  are the coordinates of the vertex,
are the coordinates of the vertex,  , of the parabola and
, of the parabola and  is the distance from the vertex to the focus and the vertex to the directrix.
is the distance from the vertex to the focus and the vertex to the directrix.
In the following equations
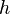 and
and  are the coordinates of the vertex,
are the coordinates of the vertex,  , of the parabola and
, of the parabola and  is the distance from the vertex to the focus and the vertex to the directrix.
is the distance from the vertex to the focus and the vertex to the directrix.Vertical axis of symmetry
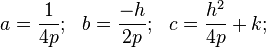
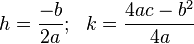 .
.
Horizontal axis of symmetry
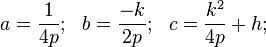
 .
.
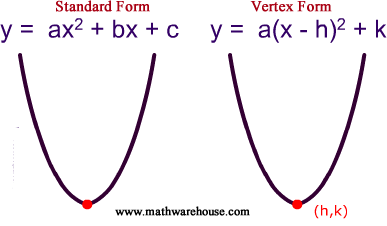
General parabola
The general form for a parabola is .
.
Latus rectum, semilatus rectum, and polar coordinates
In polar coordinates, a parabola with the focus at the origin and the directrix parallel to the y-axis, is given by the equation
where l is the semilatus rectum: the distance from the focus to the parabola itself, measured along a line perpendicular to the axis of symmetry. Note that this equals the perpendicular distance from the focus to the directrix, and is twice the focal length, which is the distance from the focus to the vertex of the parabola.
The latus rectum is the chord that passes through the focus and is perpendicular to the axis of symmetry. It has a length of 2l.Gauss-mapped form
A Gauss-mapped form: 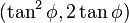 has normal
has normal 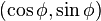 .
.
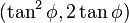 has normal
has normal 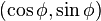 .
.




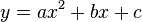









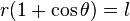
0 comments:
Post a Comment