To derive the focus of a simple parabola, where the axis of symmetry is the y-axis with the vertex at (0,0), such as
FP, a line from the focus to a point on the parabola, has the same length as QP, a line drawn from that point on the parabola perpendicular to the linear directrix, intersecting at point Q.
Imagine a right triangle with two legs, x and f-y (the vertical distance between F and P). The length of the hypotenuse, FP, is given by
The line QP is given by adding y (the vertical distance between the point P and the x-axis) and f (the vertical distance between the x-axis and the linear directrix).
FP, a line from the focus to a point on the parabola, has the same length as QP, a line drawn from that point on the parabola perpendicular to the linear directrix, intersecting at point Q.
Imagine a right triangle with two legs, x and f-y (the vertical distance between F and P). The length of the hypotenuse, FP, is given by
The line QP is given by adding y (the vertical distance between the point P and the x-axis) and f (the vertical distance between the x-axis and the linear directrix).


 can be written as
can be written as 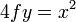 ; and for a parabola such as f(x)=x², the a coefficient is 1, so the focus F is (0,¼)
; and for a parabola such as f(x)=x², the a coefficient is 1, so the focus F is (0,¼)
As stated above, this is the derivation of the focus for a simple parabola, one centered at the origin and with symmetry around the y-axis. For any generalized parabola, with its equation given in the standard form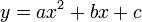 ,
,



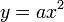
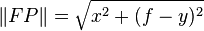
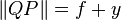


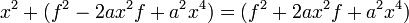
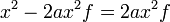
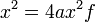
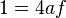
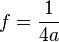
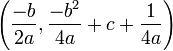



0 comments:
Post a Comment