A family of confocal hyperbolas is the basis of the system of elliptic coordinates in two dimensions. These hyperbolas are described by the equation
where the foci are located at a distance c from the origin on the x-axis, and where θ is the angle of the asymptotes with the x-axis. Every hyperbola in this family is orthogonal to every ellipse that shares the same foci. This orthogonality may be shown by a conformal map of the Cartesian coordinate system w = z + 1/z, where z= x + iy are the original Cartesian coordinates, and w=u + iv are those after the transformation.
Other orthogonal two-dimensional coordinate systems involving hyperbolas may be obtained by other conformal mappings. For example, the mapping w = z2 transforms the Cartesian coordinate system into two families of orthogonal hyperbolas



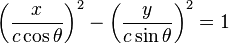
0 comments:
Post a Comment