Rectangular hyperbolas with the coordinate axes parallel to their asymptotes have the equation
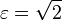 ) with semi-major axis and semi-minor axis given by
) with semi-major axis and semi-minor axis given by  .
.
The simplest example of rectangular hyperbolas occurs when the center (h, k) is at the origin:
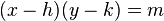 .
.
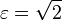 ) with semi-major axis and semi-minor axis given by
) with semi-major axis and semi-minor axis given by  .
.The simplest example of rectangular hyperbolas occurs when the center (h, k) is at the origin:
describing quantities x and y that are inversely proportional. By rotating the coordinate axes counterclockwise by 45 degrees, with the new coordinate axes labelled 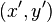 the equation of the hyperbola is given by canonical form
the equation of the hyperbola is given by canonical form
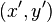 the equation of the hyperbola is given by canonical form
the equation of the hyperbola is given by canonical form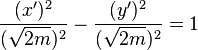 .
.



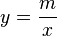
0 comments:
Post a Comment