The tangent of the parabola described by equation y=ax2 has slope
 .
.
Let a light beam travel down the vertical line TP and bounce off from P. The beam's angle of inclination from the mirror is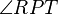 , so when it bounces off, its angle of inclination must be equal to
, so when it bounces off, its angle of inclination must be equal to 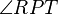 . But
. But 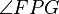 has been shown to be equal to
has been shown to be equal to 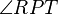 . Therefore the beam bounces off along the line FP: directly towards the focus.
. Therefore the beam bounces off along the line FP: directly towards the focus.
Consider a point, P, such that light that is initially travelling parallel to the axis of symmetry is reflected from P along a line that is perpendicular to the axis of symmetry. Since the light is turned through 90 degrees by the reflection, the slope of the parabola at P must be 1.

 .
.
Line QP can be extended beyond P to some point T, and line GP can be extended beyond P to some point R. Then 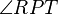 and
and 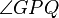 are vertical, so they are equal (congruent). But
are vertical, so they are equal (congruent). But 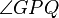 is equal to
is equal to 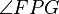 . Therefore
. Therefore 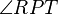 is equal to
is equal to 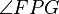 .
.
The line RG is tangent to the parabola at P, so any light beam bouncing off point P will behave as if line RG were a mirror and it were bouncing off that mirror.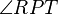 and
and 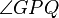 are vertical, so they are equal (congruent). But
are vertical, so they are equal (congruent). But 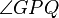 is equal to
is equal to 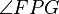 . Therefore
. Therefore 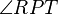 is equal to
is equal to 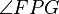 .
.Let a light beam travel down the vertical line TP and bounce off from P. The beam's angle of inclination from the mirror is
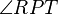 , so when it bounces off, its angle of inclination must be equal to
, so when it bounces off, its angle of inclination must be equal to 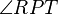 . But
. But 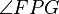 has been shown to be equal to
has been shown to be equal to 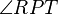 . Therefore the beam bounces off along the line FP: directly towards the focus.
. Therefore the beam bounces off along the line FP: directly towards the focus.
Conclusion: Any light beam moving vertically downwards in the concavity of the parabola (parallel to the axis of symmetry) will bounce off the parabola moving directly towards the focus. (See parabolic reflector.)
The same reasoning can be applied to a parabola whose axis is vertical, so that it can be specified by the equation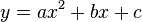 .
.
 .
.
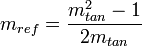 .
.
Consider a point, P, such that light that is initially travelling parallel to the axis of symmetry is reflected from P along a line that is perpendicular to the axis of symmetry. Since the light is turned through 90 degrees by the reflection, the slope of the parabola at P must be 1.


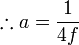
- So the equation of the parabola is
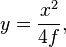 or
or 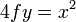




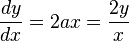
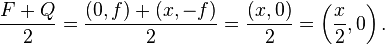
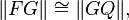

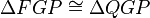
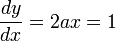
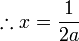
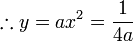
0 comments:
Post a Comment